feistel和spn结构的差分分析
feistel和spn结构的差分分析
前言
以下内容仅仅作为个人对差分分析的理解,或许具备一定的参考但是不多哈哈哈,如果发现问题师傅可以私信交流一下
差分分析介绍
引入
==为什么要在分组密码之中差分==
我们在通常的加密解密过程中,存在一些场景密钥是会被复用的.有时我们能获得一个加密装置,通过控制输入M得到输出C.如果是以最朴素的方式
$C=M\oplus Key$ 那么我们控制输入m1和得到输出c1就能得到$Key=m_{1}\oplus c_{1}$
为了防止这种事情的发生我们在分组密码中引入了多个一些线性和非线性的操作..让我们在每轮次线性和非线性的操作中无法轻易的得到key利用明文和密文.
或许只有一轮次这种操作,如图他的线性操作都可以逆,并且S盒的非线性操作都是6bit一组你可以轻松爆破,但是一旦轮次增加,就不可能利用单独的爆破对破解效率有足够的提升.
]
因为中间每一轮次都会有key的影响,或是在s盒前或是在S盒后进行与key 异或
对于多轮次的这种操作,我们需要利用差分分析来解决经过key对Sbox输入的影响,需要构造输入差分和输出差分.
基础知识
异或运算是线性的。所以如果我们知道了一对明文,(p1,p2)和一堆密文(c1,c2)
$c_1=p_1\oplus k…..c_2=p_2\oplus k$
$c_1\oplus c_2=p_1\oplus k_1\oplus p_2\oplus k_2=p_1\oplus p_2$
所以单纯的异或这样的线性运算,如果我们 知道了一堆密文,想恢复明文是很轻易的
- 差分值。
设X,X^’’^ ∈{0,1}^n^ 这个表示X是n bit的二进制数。则X和X^’’^ 的差分值的定义为$\Delta X=X\oplus X^{‘’}$
- 差分对
$设\alpha 和\beta∈[0,1]^{n} 假设\alpha 表示输入对(X,X^{‘’} ) X\oplus X^{“} =\alpha$
$经过某种i轮运算得到的输出Y_i=F(X),Y_i^{‘’}= F(X^{‘’}) 得到的\beta =Y\oplus Y^{‘’} 那么我们称(\alpha,\beta) 为到第i轮的差分对$
- 差分特征
迭代分组密码的一条i轮差分特征
$差分特征\Omega=({\beta_0,\beta_1,..,\beta_{i-1},\beta_i}) 用输入差分值X \oplus X^{‘’}=\alpha =\beta_0 ,\在i轮加密过程中,中间状态(Y_j,Y_j^{‘’}) 的差分值为Y_J \oplus Y_J^{‘’}=\beta_j,差分特征表示的是整轮每个的数据这也是跟差分对的区别$
- 差分概率
$当输入差分值为\alpha 经过i轮运算得到输出的\beta的概率表示(\alpha,\beta)的差分概率DP(\alpha,\beta)$
- 差分特征概率
$迭代分组密码一组差分特征\Omega=(\beta_0,\beta_1,..,\beta_{i-1},\beta_i) ,差分特征概率DP(\Omega)=DP(\beta_0,\beta_1)*DP(\beta_1,\beta_2)….DP(\beta_{i-1},\beta{i})$
可以看出,差分特征概率会在意过程中得到的差分值
活跃S盒(Active S-box):
在密码算法的某一轮(或某一步骤)中,若某个S盒的输入差分(或线性掩码)不为零,则该S盒被称为活跃S盒。活跃S盒会对输出的差分(或线性特性)产生直接影响。非活跃S盒(Inactive S-box):
若某个S盒的输入差分(或线性掩码)为零,则该S盒被称为非活跃S盒。此时,S盒的输出差分也为零(假设S盒是双射的),因此不会对后续轮次的差分传播产生贡献。正确对与错误对
我们选择合适的路径作为区分之后堆叠数量自动过滤
DES 差分分析
feistel结构
feistel cipher是用来构建分组加密算法的对称结构,很多经典的分组加密都会用到这个比如这里的DES
这个算法中将一直的明文分成两半,一半先保留(L),另一半R被加密。存在一个轮函数f用于加密。F(L,k)用来计算后与R异或用于加密每一轮的R,然后R再与L交换位置一次类推。在传统的DES中这样的计算要进行16次
这样做解密时也十分方便,将过程反过来即可。
为什么可以直接解密,原理非常简单网上到处都是这里不过多追述
- DES的过程不过多赘述,相信详情可以网上自查
S盒分析
- 接下来我们对S盒子中第一个表进行分析;
我们回顾一下DES中的S盒加密过程
在与密钥k异或置换,再S盒压缩
我们现在想要知道密钥Ki,已经知道了E盒扩展后的输入(p1,p2),p经过k异或后记作b1和b2,p和S盒压缩后的输出(c1,c2)。
我们记$p1\oplus p2=b1\oplus b2=P,c1\oplus c2=C。$
P是最多6bit的数,C最多是4bit。
- 解释一下S盒分析的定义:
对于输入的P,有64中可能,对于输出的C有16种可能,并且S盒是非线性的。分布的对应XOR,P和C往往是不规律的。
例如这里我们可以对S1盒进行分析
1 | |
1 | |
我们便可以得到S1盒的相关差分分析,并且我们这里还能得到每一个对应XOR可能的输入B。
- 接下来我们尝试恢复经过S盒前的Key
p1–>key—>B–>[S盒]–>key;
假设我们知道两对数据。p1和p2以及p_1和p_2。
P1=p1^p_2,
P2=p_1^p_2。
B=p1^key B*=p2^key。
B^B*=P1。
B2=p_1^key
B2*=p_2^key>
B2^B2*=P2。。。
C1=S_x(B)^S_x(B*),C2=S_x(B2 )^S_x(B2 *)
我们需要先利用最开始求到的每一对XOR对应的B求出可能的B,讲B和对应的p1异或得到可能的key。真正满足要求的key,会会同时满足两对数据的要求。不过一般情况下两对恢复的精确度是不够的,我这里代码使用了5对这样的数据。
find_key。
1 | |
利用所有可能的输入找到key。
补充
类似这种只对S_box分析的讨论是无意义的,我们更多的是必须在如何更好的爆破被多轮次混淆过后的代码上来.和后面的1轮次和二轮次的DES差分攻击一样,因为其实可以利用爆破的方法恢复出一轮次的key无法体现出需要差分的必要性
三轮次的DES差分分析3轮差分分析其实和一轮二轮差不多,都是对S盒进行的分析。
示例我们选择的一段明文,
(R,L) (R’,L’)
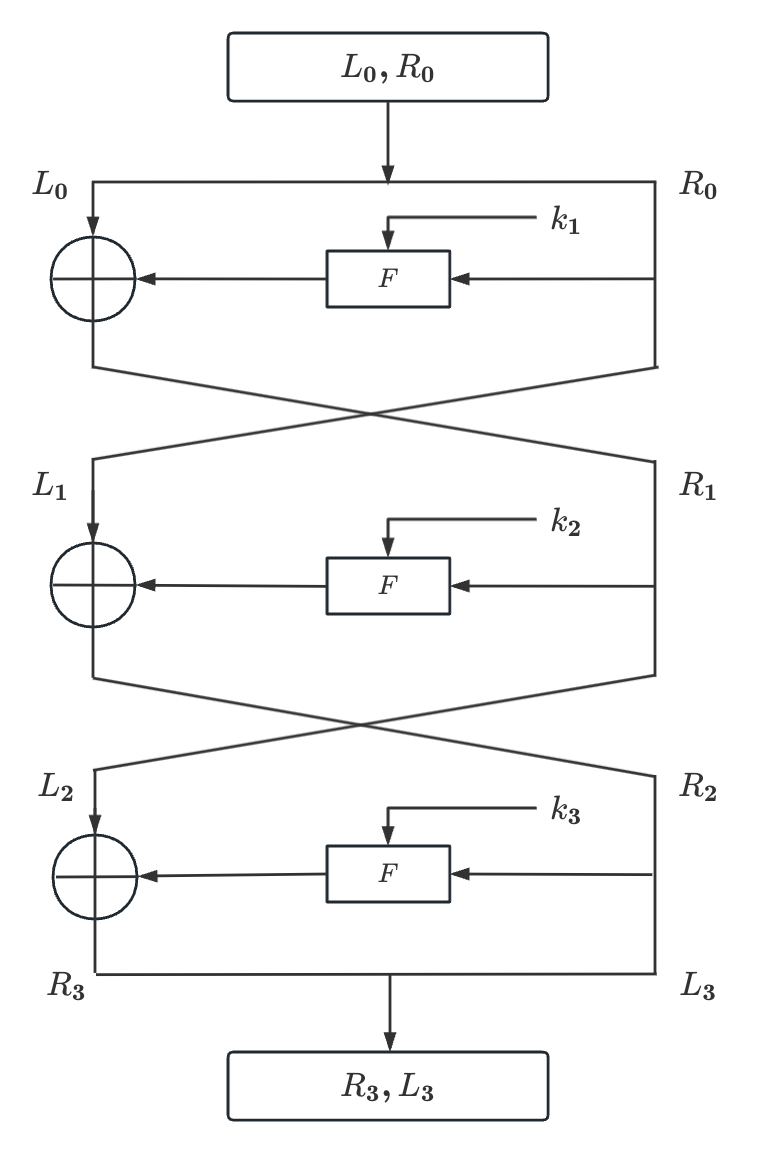
我们假设R0=R0’,
输出$R3=L2\oplus f(R2,k2)=R1\oplus f(R2,K2)=L_0\oplus f(R0,k1)\oplus f(R2,k3)$ ,
$R3’=L2\oplus f (R2’k2)=R1’\oplus f(R2’,K2)=L_0’\oplus f(R0’,k1)\oplus f(R2’,k3)$
那么可以得到,$R3^*=R3\oplus R3’= L0^* \oplus f(R_2, K_3) \oplus f(R_2’, K_3)$
我们在三轮中已知(R0,L0) (R0’,L0’)所以 ,输出差分$R3^*=L0^* \oplus f(R_2, K_3) \oplus f(R_2’, K_3)$
并且R2=L3,R2’=L3’,所以我们可以得到输入差分与输出差分的关系。
$R3^\oplus L0^= f(L3,k3)\oplus f(L3’,K3)$
我们可以,将L3/L3’被E盒转化之后视作S盒的输入。将$R3^\oplus L0^$ 逆P盒之后视作输出的异或。
1 | |
6轮次DES差分分析
差分分析采用的差分特征如图 7 所示:

选择明文满足 $L_0’=40080000_x$ 和 $R_0’=04000000_x$ 的明密文对 $(L_0R_0, L_6R_6)$ 和 $(L_0^R_0^, L_6^R_6^)$,$R_6$ 和 $R_6^*$ 可分别表示为:
$R_6 = L_5 \oplus f(R_5, K_6)=R_4 \oplus f(R_5, K_6)=L_3 \oplus f(R_3, K_4) \oplus f(R_5, K_6) \ R_6^* = L_5^* \oplus f(R_5^*, K_6)=R_4^* \oplus f(R_5^*, K_6)=L_3^* \oplus f(R_3^*, K_4) \oplus f(R_5^*, K_6)$
因此有:
$R_6’=L_3’ \oplus f(R_3, K_4) \oplus f(R_3^*, K_4) \oplus f(R_5, K_6) \oplus f(R_5^*, K_6)$
$R_6’$ 是密文差分的左半部分,从上述构造的差分特征 $\Omega$ 中,由给定明文差分得到第 3 轮的密文差分的概率为 $1/16$。如果情况确实如此,那么第 4 轮 $S$ 盒的输入差分可以通过轮函数扩展 $E$ 计算得到:$001000 | 000000|000001|010000 |000000 |000000 |000000 |000000 $
观察到 $S_2, S_5, S_6, S_7, S_8$ 的输入差分全为 0,因此在第 4 轮中这五个 $S$ 盒的输出差分全为0。根据 $P(C_6’)=f(R_5, K_6) \oplus f(R_5^*, K_6), P(C_4’)=f(R_3, K_4) \oplus f(R_3^*, K_4)$,代入 $R_6’$,可以得到:
$P(C_6’)=R_6’ \oplus L_3’ \oplus P(C_4’)$
故 $C_6’=P^{-1}(R_6’ \oplus 04000000_x) \oplus (*0**0000_x)$
据此我们得到第 6 轮轮函数五个非活跃 $S$ 盒的输出差分,而其输入差分可以通过 $B_6=E(L_6),B_6^*=E(L_6^*)$ 计算出来,这样我们得到了攻击 $S$ 盒的三元组 $(B_6,B_6^*, C_6’)$,然后我们采用如下攻击流程来攻击第 6 轮轮函数的 5 个 $S$ 盒:
- 计算 $C_6’=P^{-1}(R_6’ \oplus 04000000_x)$
- 计算 $B_6 = E(L_6), B_6^*=E(L_6^*)$,然后计算 $B_6’=B_6 \oplus B_6^*$
- 对于 $i \in {2, 5, 6, 7, 8}$,计算子密钥部分比特 $J_i \in KJ_i, KJ_i = IN_S(B_{6,i}’, C_{6,i}’) \oplus B_{6,i}$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40from os import urandom
from Crypto.Util.number import bytes_to_long
from DES import *
from tqdm import *
def find_key3(M,M1,C):
KEY=[]
for i in range(8):
k=find_key(C,M,M1,len(M),i)
KEY.append(k)
return KEY
if __name__ == "__main__":
key = b"8bytekey" # 8 字节密钥
MSG=[]
MSG1=[]
Cip=[]
l=0
key2=split48(193047425125744)
for i in tqdm(range(100)):
M=bytes.fromhex("4008000004000000")
print(len(M))
M1=urandom(8)
M2=bytes_xor(M,M1)
C1=des_ecb_encrypt1(key,M1,6)
C2=des_ecb_encrypt1(key,M2,6)
C=bytes_xor(C1,C2)
L3_1=C1[4:]
L3_2=C2[4:]
a=bytes.fromhex("04000000")
MSG1.append(permute(bytes_to_long(L3_1),E,32))
MSG.append(permute(bytes_to_long(bytes_xor(L3_1,L3_2)),E,32))
R3=bytes_xor(C1[:4],C2[:4])
Cip.append(permute(bytes_to_long((bytes_xor(R3,a))),P_INV,32))
KEY=find_key3(MSG,MSG1,Cip)
print(KEY)
print(l/100)
print(key2)
SPN(Substitution-Permutation Network)结构的差分分析
SPN结构这里我们参考AES设定了一个Sbox[0-256] 依次打乱顺序,然后P盒用于置换,其实就是SPN意思的来源,
SPN结构(代换-置换网络)是一种常见的分组密码加密算法结构,主要用于实现加密和解密过程。其基本思想是将明文分成若干个固定长度的块,然后对每个块进行加密。SPN结构包含三个主要部分:
代换层:通过S盒(Substitution Box)实现明文的代换操作,将明文的每个字节替换成另一个字节。
置换层:通过P盒(Permutation Box)实现明文的置换操作,将明文的每个字节的位置进行置换。
密钥加层:将密钥与中间结果进行异或操作,以增强安全性。
SPN结构的代表算法是IDEA(IBM的高级加密标准),它使用64位长度的块和128位长度的密钥,并进行了8.5轮迭代运算
这里我们
输入M->P(代换)->S(置换)->KEY异或 –…….重复几轮次1
2
3
4
5
6
7
8
9
10
11
12
13def f_cry(key,M):
M=P_ex(M)
M=S_all(M)
M=key^ M
return M
def encrypt(M,KEY):
for i in range(3):
M=f_cry(KEY[i],M)
return M
三轮次SPN结构的差分分析
spn这种结构其实对于差分抗性非常好,如果是AES的Sbox四轮就爆破不了了,aes的S盒子的差分分析表每个输入对应的每个输出分布的非常平均.这里我自己设定了一个十分不安全的Sbox,
因为SPN结构和feiste结构的区别,我们的解密分析的方式有点区别
我们获取$M$作为一对输入的差分,$C_{1},C_{2}$,分别作为输出差分$C=C_{1}\oplus C_{2}$
我们通过寻找一条合理的路径固定第三轮的输入差分为$M$ ,$C_{1},C_{2}$ ,
通过测试每个可能的某个字节的key
$M=INV_S(C_{1}\oplus key)\oplus INV_S(C_{2} \oplus key)$ 这个进行判断来筛选出最可能key
不过差分分析最艰难的过程其实是找到一组合适的差分路径.长度越长,找出合适的差分路径难度越大,并且找出概率比较高,所需数据数量少的也会变难
1 | |
代码详情见https://github.com/rockfox0/Differential-Analysis
参考
https://www.ioactive.com/wp-content/uploads/2015/07/ldc_tutorial.pdf
https://link.springer.com/article/10.1007/BF00630563

